Observer l’Univers qui l’entoure, depuis le plus petit grain de sable jusqu’à l’étoile lointaine, a, de tout temps, passionné l’Homme. Une manière certaine de se situer, d’expliquer sa présence, d’anticiper son avenir peut-être. Mais l’observation n’est que le début : homo sapiens, grâce à son cerveau capable d’abstraction, a presque aussitôt cherché à le comprendre, cet Univers, à le décrypter, à l’interpréter. Pour cela, il devait identifier les grandes lois physiques et mathématiques qui expliquent son agencement. Durant des siècles, s’affranchissant peu à peu des obscurantismes et des préjugés, les scientifiques ont bâti des théories, accumulé des expériences, édifié des modèles, amassé patiemment certitudes et probabilités. Après Newton, c’est Albert Einstein qui, le premier, réussit à expliquer de façon convaincante l’une des quatre grandes forces de notre environnement, la gravitation, dans sa théorie de la relativité générale (voir sujet : théorie de la relativité générale). Les trois autres forces fondamentales (interaction faible, interaction forte et électromagnétisme : voir sujet : les constituants de la matière) furent unifiées par la mécanique quantique (voir sujet : mécanique quantique) quelques années plus tard. Tout est donc parfait ? Hélas non car ces deux théories, la relativité einsteinienne et la physique des quantas, sont complètement incompatibles... Or, si l’on veut vraiment connaître les mécanismes régissant l’Univers dont nous faisons partie, il est indispensable d’avoir une explication physique globale : il est en effet peu probable que l’Univers réponde à des lois différentes selon l’endroit ou les niveaux d’où on l’observe. Vers la fin du siècle dernier, un certain nombre de théories unificatrices ont vu le jour et la plus prometteuse d’entre elles semble être la théorie des cordes.

Genèse de la théorie des cordes

     Vers 1950, il n’était toujours pas possible de comprendre vraiment la physique des particules plus petites que l’atome, particules que l’on appelle des hadrons (il s’agit en fait de particules élémentaires comme les quarks constituant protons et neutrons eux-mêmes formant le noyau des atomes, les gluons responsables de l’interaction forte entre les quarks, etc.). Tout ce petit monde fort complexe est bien régi par la mécanique quantique mais sans que l’on ait d’explication véritable sur leurs interactions. Il faudra attendre 1973 et l’arrivée d’une nouvelle théorie, la chromodynamique quantique, pour y voir un peu plus clair mais de façon encore partielle.

     C’est environ 10 ans plus tard que l’on entend réellement parler de la théorie des cordes qui se propose – puisque les particules restent en grande partie mystérieuses – de les penser autrement : dans cette théorie, les entités basiques de la physique, ces fameuses particules subatomiques, ne sont plus considérées comme des objets ponctuels mais comme des cordes infinitésimales formant des boucles qui vibreraient en possédant une tension, tout comme un élastique dont la tension s’accroit au fur et à mesure qu’on l’étire. Rappelons-nous que chaque particule subatomique est identifiée par son spin, c'est-à-dire une caractéristique particulière qui lui est propre (comme, également, la charge électrique ou la masse) représentant ici l’énergie cinétique de la particule tournant sur elle-même autour d’un axe. La théorie des cordes prétend que ce sont ces vibrations à des fréquences diverses qui expliquent les variations de spins observées et donc les différentes particules. Du coup, les divers types de cordes et leurs vibrations multiples seraient à l’origine de toutes les particules élémentaires de notre univers. Bien entendu, la théorie s’appuie sur de savantes équations mathématiques (notamment la théorie des surfaces de Riemann) que je serais bien en peine ici d'expliquer… Quoi qu’il en soit, il s’agit là d’une remise en cause complète, et de notre perception, et de notre compréhension de la physique subatomique.

Une théorie séduisante mais pas encore démontrée

     Les spécialistes de la question le disent et on les croit : pour permettre l’unification des deux grandes physiques, la théorie des cordes doit satisfaire à trois conditions principales :

    1. toutes les particules subatomiques sans exception doivent entrer dans le cadre de la théorie ;

     2. la théorie doit parfaitement décrire la gravitation 

     3. ce qui entraîne le fait qu’il doit s’agir d’une théorie géométrique, seul moyen de prendre en compte  cette gravitation.

     Que disent les équations de la théorie des cordes ? Que les trois conditions qu’on vient de voir lui sont tout à fait accessibles… à la condition qu’on considère un espace-temps à au moins dix dimensions ! Ce qui pose problème puisque dans notre univers (en tout cas pour sa partie visible) il n’existe que quatre dimensions ! L’ennui est que lorsqu’on revient à quatre dimensions, l’unicité de la théorie si intéressante disparaît… La cohérence mathématique de la théorie exige donc plus de dimensions qu’il ne semble y en avoir dans notre monde : ses partisans nous affirment que, en réalité, ces dimensions supplémentaires existent bel et bien mais qu’elles sont enroulées au niveau microscopique, un niveau des millions de fois inférieur à celui de l’atome. Cette affirmation doit être évidemment prouvée avant de valider la théorie : le retour (mathématique) à un espace-temps à quatre dimensions est donc le grand défi que s’efforcent de vaincre les chercheurs actuels de la théorie des cordes.

Une théorie unificatrice et ses conséquences

     Une chose est en tout cas certaine : la théorie des cordes (qui est en fait l’amalgame de plusieurs théories prenant en compte des cordes de natures différentes) semble être l’entreprise conceptuelle actuellement la plus à même d’associer la gravitation à la mécanique quantique et il est donc normal que cette aventure – extraordinairement théorique – passionne non seulement les chercheurs de physique fondamentale mais également les mathématiciens… et les astronomes.

     D’ailleurs, comme le lecteur l’aura certainement remarqué, j’ai fait figurer ce sujet non pas en physique (comme la mécanique quantique, par exemple) mais dans la catégorie des sujets d’astronomie et il y a de bonnes raisons à cela : de grandes interrogations existent toujours sur des phénomènes astronomiques importants tout simplement parce qu’on ne sait pas associer mécanique quantique et relativité générale.

          *  C’est par exemple, le cas des trous noirs. Voilà des objets dont on connait l’existence et dont on peut même mettre en évidence la réalité (du moins de façon indirecte puisque, par sa seule présence, un trou noir modifie la partie d’univers qui l’entoure) mais qu’on ne sait pas expliquer complètement (voir sujet : trous noirs).

      Pour mémoire, je rappelle qu’un trou noir est le stade évolutif terminal de très grosses étoiles : en effet, si la masse d’une étoile dépasse quarante fois celle de notre Soleil (MS), son noyau résiduel dégénéré peut dépasser les trois MS. En pareil cas, les forces de répulsion des composants atomiques dégénérés (neutrons et protons) ne peuvent plus s'opposer à la compression des forces gravitationnelles et la matière s’écrase sur elle-même sans que plus rien ne s’y oppose : on aboutit alors à la formation d’un trou noir dont la principale caractéristique est qu’aucune matière – pas même la lumière – ne peut s’en échapper. Avant l’anéantissement, on peut observer le disque d’accrétion, sorte de dernier ballet de la matière appelée à disparaître et qui dessine les abords du trou noir par l’échauffement gigantesque qu’elle subit (ce qui permet de repérer le phénomène). Puis, cette matière est absorbée par le trou noir, sans espoir de retour, et le moment où elle bascule vers l’inconnu se situe à ce que l’on nomme l’horizon du trou noir, dernière ligne encore visible avant le néant. Que devient-elle ensuite ? Ni la physique quantique, ni bien sûr la relativité ne peuvent répondre. Voilà donc un domaine où la théorie des cordes pourrait nous rendre de sérieux services…

          * Un autre sujet – et non des moindres – qui passionne les astronomes, notamment ceux qui s’intéressent à la cosmologie, est le Big-Bang. Ou, pour être encore plus général, le début de notre univers. Dans le sujet dédié (voir : Big bang et origine de l’Univers), nous avions vu que, en remontant le temps jusqu’aux origines, à partir d’un certain moment appelé temps de Planck, très précisément à 10^-43 seconde après le début, les quatre forces fondamentales que nous avons évoquées plus haut sont fusionnées en une force unique, la supergravité. A cet instant, très court mais si important, les lois de la physique classique ne s’appliquent plus (ou pas encore). La théorie des cordes serait elle susceptible de nous aider à comprendre comment tout a commencé ?

     D’autres problèmes d’astronomie restent – si j’ose dire – en souffrance et on aimerait bien une théorie (en fait un ensemble de lois mathématiques conduisant à un modèle qu’il serait possible d’expérimenter par la suite) nous permettant de les expliquer…

La théorie des cordes a-t-elle un intérêt autre que… théorique ?

     La réponse est à l’évidence oui ! S’acharner à unifier des théories physiques compliquées en une théorie encore plus complexe ne relève pas d’un simple jeu mathématique pour quelques initiés, fussent-ils géniaux. Les retombées d’une telle entreprise, si elle devait aboutir, seraient considérables. Evidemment, comme on vient de le voir, ou pourrait en apprendre énormément sur notre Univers (et donc sur nous-mêmes) mais pas seulement. Il suffit de se rappeler combien la physique quantique a été décriée à ses débuts : certains scientifiques criaient à la mystification, ne pouvant comprendre comment on pouvait tirer des lois à partir du pur hasard ; d’autres riaient à la lecture de qu’ils considéraient comme un salmigondis. D’autres encore, plus sages peut-être comme le grand Einstein lui-même, préféraient attendre dans une prudente réserve teintée de scepticisme. Et pourtant ! Sans mécanique quantique, pas de contrôle de l’électron et donc ni transistors, ni informatique. Pas non plus de supraconduction et d’imagerie médicale de type résonnance magnétique nucléaire (IRM). Sans elle, on ne saurait toujours pas contrôler la lumière pour réaliser les faisceaux laser de nos lecteurs de DVD. Même chose pour les centrales nucléaires… La mécanique quantique, si mal comprise car si imprévisible et apparemment si contraire à notre logique, a transformé notre monde.

      Si l’on arrive à écrire des équations universelles de la théorie des cordes et à formaliser la théorie unificatrice, les conséquences pratiques – impossibles évidemment à imaginer aujourd’hui - en seront certainement considérables. Au-delà de la satisfaction d’avoir compris un peu plus notre univers, les transformations de notre quotidien seront telles qu’il faut souhaiter de l’intuition, beaucoup de patience et peut-être un peu de chance à ces chercheurs si particuliers.

Images

1. galaxie NGC 4945 (sources : www.eso.org)

2. constituants de l'atome (sources : abyss.uoregon.edu)

3. cordes (sources : hypersite.free.fr/)

4. univers multidimensionnel (sources : techno-science.net) 

5. dessin d'un trou noir (sources ; paturage.files.wordpress.com)

6. simulation des premiers instants de l'Univers (sources : irfu.cea.fr/)

7. homecinema (sources : le-showroom.ecranlounge.com)

  (Pour lire les légendes des illustrations, passer le pointeur de la souris dessus)

Mots-clés :  relativité générale - mécanique quantique - hadron - quark - gluon - chromodynamique quantique - trou noir - Big bang - supergravité  - temps de Planck - théorie unificatrice de la physique - théorie des cordes (compléments)

  (les mots en gris renvoient à des sites d'informations complémentaires)

Articles connexes sur le blog :

* Big bang et origine de l'Univers

* théorie de le relativité générale

* mécanique quantique

Dernier sommaire général du blog : cliquer ICI

l'actualité du blog se trouve sur FACEBOOK

 Mise à jour : 8 mars 2023

      La disparition des grands sauriens date de – 65 millions d’années et elle s’est faite rapidement, en quelques milliers d’années, ce qui est très court comparé à leur règne qui s’étale sur plus de 150 millions d’années. On a expliqué dans des sujets précédents combien il était probable que cette disparition a été hâtée par la chute d’une météorite géante sur des populations déjà en déclin (voir sujets : la disparition des dinosaures et l'empire des dinosaures). Quoi qu’il en soit, une niche écologique majeure s’est trouvée libérée pour des successeurs potentiels qui vivaient jusque là dans l’ombre, les mammifères.

     Il est néanmoins intéressant de noter qu’une compétition s’engagea assez rapidement entre deux types de mammifères : les placentaires et les marsupiaux, l’Evolution ayant donné dans chacun de ces deux groupes des individus également armés comme on le verra ensuite (on parle alors d’évolution parallèle, c’est-à dire l’acquisition de caractéristiques semblables dans deux espèces occupant un même espace, à ne pas confondre avec une évolution convergente qui donne des attributs identiques à deux populations existant à des époques ou dans des écosystèmes différents).

Placentaires et marsupiaux

     Les mammifères sont pratiquement contemporains des dinosaures. Toutefois, dès le début, la suprématie des grands sauriens se révèle indiscutable et les mammifères doivent se contenter de la portion congrue : à cette époque, ils sont représentés par de petits vertébrés à sang chaud (dont certains possèdent une fourrure) et qui, vivant principalement la nuit, se nourrissent d’insectes, de vers et parfois… d’œufs de dinosaures.

     Tout change pour les mammifères à la fin du crétacé, très précisément lors de ce que l’on nomme la " limite KT ", où une extinction massive touche nombre d’espèces vivantes, au premier rang desquelles les dinosaures. On entre alors dans le cénozoïque (ancienne époque tertiaire) dont les premiers millions d’années sont le paléogène et c’est à partir de cette époque lointaine que va se développer la « radiation » des mammifères, c'est-à-dire leur conquête de tous les milieux laissé vacants par leurs gigantesques prédécesseurs. Rapidement deux sous-classes de mammifères apparaissent, les placentaires et les marsupiaux, vraisemblablement à partir d’une souche commune originaire d’Amérique du nord, et probablement en raison, à cette époque, de l’isolement  des continents (voir le sujet : dérive des continents ou tectonique des plaques), ils ne rentreront véritablement en compétition que plus tardivement.

          *  mammifères marsupiaux

     Chez les marsupiaux (du grec marsipos = sac), la femelle possède une poche ventrale dans laquelle, peu après sa naissance, se développe son petit. En effet, point important, après environ 3 semaines,  l’enfant marsupial se retrouve extériorisé sous la forme d’un fœtus très primitif au point que certains scientifiques l’ont baptisé « larve marsupiale ». L’enfant devra donc procéder à son développement définitif dans la poche externe de sa mère. C’est dire que cette croissance - qui prendra plusieurs mois - laisse la femelle et son petit très vulnérables à la prédation.

     Il existe encore aujourd’hui un peu moins de 300 espèces différentes de marsupiaux, notamment des kangourous (mais dont le nombre d’espèces est passé en 150 ans de 42 à moins de 15). Les kangourous sont les plus grands marsupiaux toujours vivants mais, au paléogène et jusqu’à assez récemment, existaient des espèces bien plus grandes, parfois de la taille d’un hippopotame, herbivores (comme le diptrodon ou le Nototherium) ou carnivores comme le thylacosmilus qui était une sorte de tigre à dents de sabre marsupial dont le poids pouvait dépasser les 100 kg.

          *  mammifères placentaires

     Ils représentent l’immense majorité des mammifères et c’est de ce groupe d’animaux dont nous sommes issus. A la différence des marsupiaux que nous venons d’évoquer, les placentaires – comme leur nom l’indique – ont une gestation totalement intra-utérine : les petits sont ainsi bien plus longtemps protégés de toute agression extérieure en  se développant au sein d’un sac interne à la mère, le placenta. La liaison avec celle-ci se fait au moyen du cordon ombilical et du liquide amniotique dans lequel baigne le petit : il s’agit donc là d’une protection maximale mais pas seulement car le placenta a bien d’autres rôles. Il permet en effet une nutrition complète en différents éléments (sucres, minéraux, acides aminés, etc.) mais aussi une certaine fonction respiratoire, le recyclage des déchets (fonction excrétrice) et une activité hormonale (fonction endocrine). Signalons aussi que le placenta a un rôle majeur en immunologie en assurant une barrière entre l’enfant et le monde extérieur. On comprend donc aisément que la gestation paraît mieux protégée chez les placentaires que les marsupiaux. Cela explique-t-il la plus grande réussite des placentaires dans leur colonisation de la Terre ? En effet, ils sont présents partout dans le monde, non seulement sur la terre ferme mais aussi dans les océans (cétacés) et même dans l’air (chauve-souris ou chiroptères dont on oublie souvent que c’est le deuxième « ordre » de mammifères le plus nombreux, juste derrière les rongeurs).

Compétition entre mammifères

     A la fin du crétacé n’existaient probablement que 200 à 300 espèces de mammifères regroupées en un peu moins de 30 familles dont 1/3 était représenté par les placentaires, 1/3 par les marsupiaux, le dernier tiers relevant d’espèces n’ayant pas survécu. A cette époque, les donnes étaient équivalentes entre les deux grands groupes de mammifères. Survient alors la disparition des dinosaures et la radiation évolutive (on peut même parler « d’explosion évolutive ») des mammifères qu’on retrouve partout en quelques dizaines de milliers d’années. D’un point de vue très schématique, on peut dire que les placentaires ont surtout dominé les continents du nord tandis que les marsupiaux se trouvent en position de force dans l’hémisphère sud (à l’exception du continent africain où ils n’ont jamais été présents).

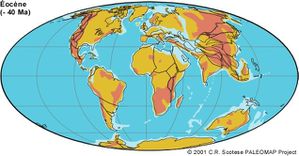     C’est à la fin du trias que le supercontinent occupant jusque là la Terre, la Pangée, commence à se fractionner. On peut supposer que cette dislocation a permis durant longtemps la non-communication et donc l’absence de compétition entre les deux grands groupes de mammifères. Vient alors la formation de l’isthme de Panama qui permet l’irruption des placentaires vers le sud où ils vont progressivement remplacer les marsupiaux. D’un point de vue anatomique, les marsupiaux n’étaient pas réellement désavantagés ; le tigre marsupial à dents de sabre (thylacosmilus) devait certainement être aussi redoutable que son cousin placentaire, le smilodon. Pourtant rapidement les placentaires triomphent, ne laissant en Amérique du sud que quelques rares niches écologiques aux marsupiaux. Pour expliquer ce succès, la seule explication qui vient à l’esprit est celle de la différence liée à la gestation des petits qui, comme on l’a vu, semble plus performante chez les placentaires.

     L’Australie, restée isolée, est le dernier continent où dominent les marsupiaux. C’est à l’Homme que l’on doit la triste réalité du déclin des marsupiaux sur ce continent. La colonisation humaine coïncide avec l’introduction de mammifères placentaires tels certains herbivores, le chat, le lapin, etc. qui vont progressivement faire régresser les espèces autochtones endémiques. Ajoutons à cela une lutte sans discernement, pour des raisons essentiellement économiques, contre les marsupiaux : ces espèces sont aujourd’hui protégées mais il est déjà trop tard pour nombre d’entre elles (on pense notamment au chien marsupial dit loup de Tasmanie dont le dernier représentant fut exterminé en 1936).

La compétition interspécifique, fer de lance de l’Evolution

     Si l’on met de côté le rôle néfaste de l’Homme en Australie dont la prédominance exclusive a rompu la stabilité de l’écosystème naturel, force est de constater que partout où les marsupiaux ont rencontré les placentaires, ce sont ces derniers qui ont pris le dessus. Certes, il s’est parfois agi de dissemblances morphologiques et comportementales : le tigre marsupial à dents de sabre par exemple, était dans l’ensemble moins rapide et moins lourd que le smilodon, son concurrent placentaire. Cela n’explique toutefois pas tout. La vraie différence entre ces différentes espèces réside dans le mode de gestation, forcément défavorable comme on la vu, aux marsupiaux. L’Evolution, on l’a souvent répété, entraine la survie du plus apte, celle de l’individu le mieux adapté à son milieu et, de ce point de vue, les marsupiaux partaient avec un handicap.

     La gestation marsupiale, par exemple, oblige à une ossification plus précoce de la boîte crânienne ce qui limite forcément le développement du cerveau de l’individu. De la même façon, la croissance de l’embryon dans une poche externe empêche l’apparition d’individus de grande taille : impossible d’imaginer une baleine marsupiale ! Or, on sait que le développement de la taille d’un individu est un élément important dans la compétition interspécifique…

     C’est également la raison pour laquelle on ne retrouve pas de grands primates marsupiaux (je ne dis pas que cela était impossible – il existe des marsupiaux d’assez grande taille – mais seulement bien plus improbable). On peut affirmer au bout du compte que, si les marsupiaux avaient pour une raison quelconque dominé leurs cousins placentaires, jamais l’Homme et son gros cerveau n’auraient vu le jour. L’Evolution se serait dirigée dans une autre direction et nous ne serions pas là pour en parler.

Images

1a. loup (canis lupus) (sources : fr.academic.ru)

1b. kangourou (sources : www.dinosoria.com)

2. dinosaures (sources : s2.e-monsite.com)

3. larve marsupiale (sources : www.mnhn.fr/)

4. foetus dans son placenta (sources : medicalimages.allrefer.com)

5. dislocation de la Pangée (sources : www2.ggl.ulaval.ca)

6. Thylacosmilus ou tigre marsupial à dents de sabre (sources : fr.wikipedia.org)

7. primate (gorille) (sources : pin.primate.wisc.edu)

(Pour lire les légendes des illustrations, passer le pointeur de la souris dessus)

Mots-clés : disparition des dinosaures - mammifères placentaires - mammifères marsupiaux - évolution parallèle - évolution convergente - crétacé - limite K-T - cénozoïque - paléogène - radiation évolutive - larve marsupiale - thylacosmilus - Pangée - smilodon - loup de Tasmanie (thylacine)

  (les mots en gris renvoient à des sites d'informations complémentaires)

  Articles connexes sur le blog :

* l'empire des dinosaures

* la disparition des dinosaures

* les mécanismes de l'évolution

* la dérive des continents ou tectonique des plaques

Dernier sommaire général du blog : cliquer ICI

l'actualité du blog se trouve sur FACEBOOK

 Mise à jour : 8 mars 2023